本文主要记录常用的一些数据结构。

源码实现

可以参考开源项目的代码，比如说linux和redis等。

通用元素表示：
C语言中一般是通过void *或者像linux那样内嵌节点实现。
C++一般是通过泛型，具体参考STL容器即可。
Go一般就是interface{}。

数组

静态数组

大小固定的数组，适合存储固定大小的数据，比如说表示月份的字符串。
底层实现只要元素个数*元素大小的内存空间即可。
在有些语言中是值语义(如Go)，直接赋值相当于内存拷贝，需要酌情使用。

动态数组

可动态调整大小的数组，一般的实现在扩容时有复制旧数据的性能开销。
可以考虑使用deque替代(内部是多个数据块拼接)。
底层实现一般是指针+实际大小+容量(可选)。
适合场景：任意位置读取、更新，以及在尾部插入、删除。

栈

适合存储后进先出的数据，操作都在栈顶。在连续的内存空间即可实现栈。
常见的函数调用、参数传递、局部变量都是栈上操作。
可以用来模拟递归调用，避免栈溢出。
在深度优先搜索中也比较常用。
简单的算术运算可以通过运算数和运算符的压栈、退栈实现。

队列

FIFO队列

适合存储先进先出的数据。
在广度优先搜索中也比较常用。
具体实现参考STL的queue或linux的sys/queue.h文件。
基于deque或者链表实现都是可以的。

优先级队列

按优先级出队，适合存储需要按优先级处理的数据。比如说TopN问题。
一般是通过大堆实现。具体实现参考STL的priority_queue。

双端队列deque

前端、后端皆可快速插入、删除的队列。
可以简单理解为多个固定大小数据块拼接而成，具体参考STL的deque实现。
适合撤消历史(环形缓冲可能更适合)或者work-stealing场景使用¹ 。

链表

可以使用冗余节点或双重指针简化插入、删除操作，快慢指针检查是否存在循环等。
配合哈希表使用，可以实现一些操作在O(1)的数据结构(比如说LRU, LFU缓存)。
链表节点一般有1~2个指针，用来存内存占用小的char、short的话就比较浪费空间了(考虑下deque吧😏)。

双向链表

可正向、反向遍历的链表，已经找到节点的情况下(有指针或迭代器)可快速删除、插入节点。

单向链表

只能正向遍历的链表，比双向链表节省空间。

循环链表

形成循环的链表，可以模拟环形缓冲。
STL的list内部通过循环链表实现。

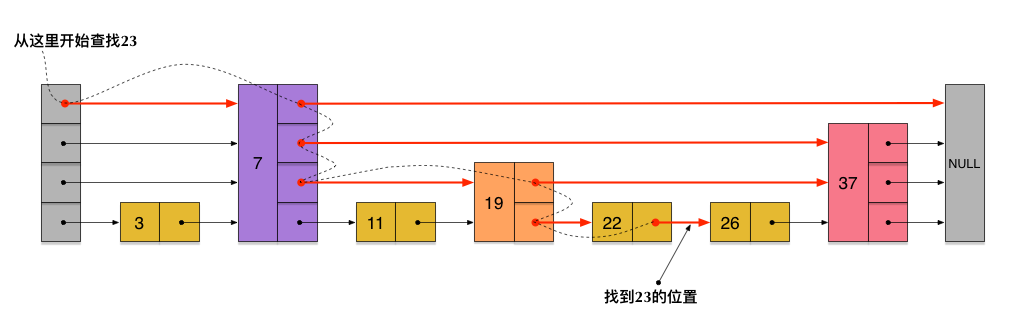
跳跃表skiplist

随机化数据结构。多层链表，加快查找、插入(随机层数)、删除操作(复杂度为logN)。
相比平衡树，在内存占用(平均指针更少)、范围查找、实现难度(增删操作)等方面有优势。
具体可以参考redis的实现以及论文《Skip Lists: A Probabilistic Alternative to Balanced Trees》。
skiplist search path

1
2
3
4
5
6
7
8


randomLevel()
    level := 1
    
    // random()返回一个[0...1)的随机数
    while random() < p and level < MaxLevel do
        level := level + 1
    
    return level

redis的实现，p为0.25，MaxLevel为32。另外第1层为双向链表。

哈希表

在冲突率不高时，查找、插入、删除可在常量时间完成。
哈希表的快速是靠空间换时间，会多耗一些内存。
在冲突率高时，需要扩容并重新哈希，建议采用类似redis那样的渐进式rehash。

多阶哈希表

通过多次哈希解决冲突、提高空间利用率的哈希表，可以通过一维数组模拟(可放入共享内存)。

Bloom Filter

快速判断元素是否在集合中。
比如说垃圾邮件过滤的场景或者辅助加速查询。
优点是速度快、省空间，缺点是有小概率误报、不能删除元素。

Cuckoo Filter

类似Bloom Filter，支持删除元素(不漏报)。

http://www.cs.cmu.edu/~binfan/papers/conext14_cuckoofilter.pdf

CQF

树

大小堆

适合存储1~N个极值的数据。
适合TopN类需求或者优先级队列、定时器的场景。

二叉堆的特性

是完全二叉树或者近似完全二叉树
父节点的键值总是 >=(或者 <=)子节点的键值
每个节点的左右子树都是二叉堆

当父节点键值总是>=子节点键值时称为最大堆，当父节点键值总是<=子节点键值时称为最小堆。
大小堆就是指最大堆和最小堆，下文主要讲述最大堆。

堆的存储

由于大小堆是(近似)完全二叉树，因此可以用数组(连续内存空间)来表示。

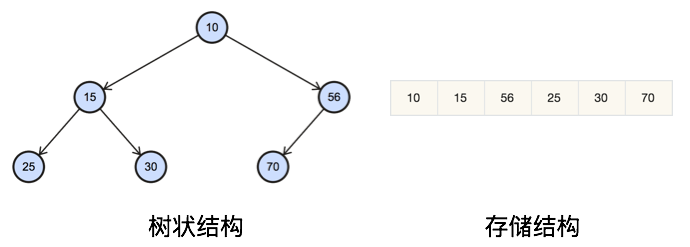
对于索引为idx的节点，其父节点索引为(idx-1)/2。
对于索引为idx的节点，其左节点索引为2*idx+1，其右节点索引为2*idx+2。

堆的元素插入

插入元素到堆都是将其放在数组最后，可以发现从新元素的父结点到根节点是有序序列，只要将其插入到这个有序序列即可。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23


void MaxHeapFixUp(vector<int>& arr, int idx)
{
    int p = (idx-1)/2; // 父节点索引

    while (0<=p)
    {
        if (arr[p] >= arr[idx])
        {
            break;
        }

        swap(arr[p], arr[idx]);

        idx = p;
        p = (idx-1)/2;
    }
}

void MaxHeapPush(vector<int>& arr, int elem)
{
    arr.push_back(elem);
    MaxHeapFixUp(arr, arr.size()-1);
}

堆的元素删除

堆只能删除堆顶元素，实际操作是把最后的元素与其交换，然后从堆顶向下调整、恢复堆。
向下调整的过程，主要是确保父节点>=子节点(最大堆)，如果不满足则跟子节点较大的进行交换。
上述过程在发生交换的情况下需要递归向下进行。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40


void MaxHeapFixDownEx(vector<int>& arr, int pretendSize, int idx)
{
    int size = pretendSize; // pretendSize <= arr.size()

    while (idx < size)
    {
        int l = 2*idx + 1; // 左节点索引
        int r = l+1;       // 右节点索引

        // 1) no children nodes
        // 2) has left child and no right child and arr[l] <= arr[idx]
        // 3) two children and arr[l] <= arr[idx] && arr[r] <= arr[idx]
        if ((l>=size || arr[l] <= arr[idx])
            &&  (r>=size || arr[r] <= arr[idx]))
        {
            break;
        }
        // at least left child exists
        int m = l;
        if (r<size && arr[r] > arr[l])
        {
            m = r;
        }

        swap(arr[idx], arr[m]);
        idx = m;
    }
}

void MaxHeapFixDown(vector<int>& arr, int idx)
{
    return MaxHeapFixDownEx(arr, arr.size(), idx);
}

void MaxHeapPop(vector<int>& arr)
{
    swap(arr.front(), arr.back());
    arr.pop_back();
    MaxHeapFixDown(arr, 0);
}

堆的建立

我们知道叶子节点是二叉堆，所以堆的建立只要从最后的非叶子节点开始往前调整堆即可。

1
2
3
4
5
6
7
8
9


void MaxHeapMake(vector<int>& arr)
{
    int idx = arr.size()/2 - 1;

    while (0<=idx)
    {
        MaxHeapFixDown(arr, idx--);
    }
}

红黑树

平衡树变种，简化插入、删除后调整树的操作。
在红黑树的基础上可以实现set、map等容器。
具体可以参考linux的实现版本。

不相交集 / 并查集

不相交集是一种可以在接近常量的时间内查询和合并的数据结构。
可以参考boost的disjoint_sets或者《算法(第四版)》1.5章节的实现。
简化版(没有参数检查)如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52


class UnionFind
{
    std::vector<int> id;
    std::vector<int> sz;
    size_t count = 0;

    int find(int p)
    {
        while (p!=id[p])
        {
            p = id[p];
        }

        return p;
    }

public:
    explicit UnionFind(int num): count(num), sz(num, 1) {
        id.resize(num);
        for (auto it = id.begin(); it != id.end(); ++it)
        {
            *it = it-id.begin();
        }
    }

    size_t size() const
    {
        return count;
    }

    bool connected(int p, int q)
    {
        return find(p) == find(q);
    }

    void connects (int p, int q)
    {
        int i = find(p);
        int j = find(q);

        if (sz[i] < sz[j])
        {
            id[i] = j;
            sz[j] += sz[i];
        }
        else
        {
            id[j] = i;
            sz[i] += sz[j];
        }
    }
};

Fenwick tree

又叫binary indexed tree，适合求prefix sum的场景。具体参考wiki上的说明。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


type fenwickTree []int

func (t fenwickTree) add(idx, val int) {
	idx++ // one-based

	for idx < len(t) {
		t[idx] += val
		idx += idx & -idx
	}
}

func (t fenwickTree) sum(idx int) int {
	sum := 0

	idx++ // one-based
	for 0 < idx {
		sum += t[idx]
		idx -= idx & -idx
	}

	return sum
}

trie树

前缀树，适合大量字符串检索、去重、前缀匹配、统计等场景。

赢家树,输家树

外部排序用到的数据结构，类似小堆可快速取出最小元素(速度快一点)。

B树系列

有待补充…

哈夫曼编码树

位图bitmap

按位存储的数据结构，节省空间，适合存储类似标志位(比如说大量用户在线状态)的数据。

Morris counter

少量内存大数据量近似计数，算法参考wiki说明。
简单来说就是只存counter的指数部分，然后类似于抛counter次硬币全部正面才加1到指数部分。

环形缓冲

环形缓冲(ringbuffer)是单读单写可无锁的数据结构，一般通过数组模拟。

可写长度为数组长度减一，区分empty和full
写入：判断是否可以写入，可以的话先写数据，然后原子修改write_index(防止torn read)
读取：判断是否可以读取，可以的话先读数据，然后原子修改read_index(防止torn read)

通过多个ringbuffer可以实现多对一的无锁通信。
这种技巧，在某T厂应用广泛。

双缓冲

空间换取并发安全的数据结构。
可以用来定时更新配置。
具体参考 DoubleBuffer 的说明。

图